Dear Mr. Manger,

In order to soothe my bad conscience a little, I examined your loudspeakers theoretically last weekend. I was surprised to find that the radiation principle chosen by you gives a radiation time history that corresponds to the time history of the current (at least in the idealisation I examined); i.e. transient oscillations and other disturbing effects do not occur. If I interpret the equations correctly, it seems feasible that a plate (membrane) with a stiffness decreasing towards the edge (thickness variation), leads to a slightly improved radiation efficiency.

With many thanks for your Christmas surprise,

Yours,
(M. Heckl)

28 January 1978

Radiation from a very pliable large plate with circular excitation

1. The problem
We consider a very large plate which is excited along a ring. The excitation force is uniform along the ring, so that the problem can be regarded as radially symmetric.

The aim is to determine the sound radiation of such a configuration, with the time history of the sound pressure being of particular interest.

»I was surprised to find that the radiation principle chosen by you gives a radiation time history that corresponds to the time history of the current (at least in the idealisation I examined)«

2. Mathematical model

In order to keep the mathematical effort low, the following assumptions are made in the calculations:

(a) The plate is large enough and strongly enough damped that the bending waves excited by the ring do not get reflected by any edge that may be present. (Because of the high damping of the material, this condition should be satisfied at least above a few hundred Hertz.)

(b) The motion of the plate can be described by the bending wave equation; i.e. membrane tensions (which would lead to nonlinearities) must be absent. (In the present configuration, this condition is probably satisfied.)

(c) The bending wavelength of the plate should be at least 25 kHz below the sound wavelength in air. (Since the material is very pliable, one can assume that the bending wavelength is below the sound wavelength by as much as about 50 kHz.)

(d) In the frequency range of interest, i.e. above about 300 Hz, the radiation loading by the surrounding air can be neglected. (Since the weight of the oscillating foil is high compared with that of loudspeaker membranes, this condition, too, should be satisfied.)

3. Calculation of the sound pressure
3.1. Basic equations

The problem is solved if solutions can be found to the sound wave equation and the bending wave equation with ring-shaped excitation, under the assumptions given above. It is known from literature [e.g. Heckl, Acustica 9 (1959), p. 371] that the sound pressure radiated by a very large plane plate is given for the radially symmetric case by the formula

The following notation has been used:

If the plate oscillates with the radially symmetric velocity distribution v(r,t) ,
then

with

ρ0 is the density of the air. If the plate is excited by a radial pressure
distribution of the form pA(r,t ), then

with

The following notation has been used:

In the present case of a ring-shaped excitation, pA is given by

hence

If equation (7) is inserted into (4) and the resulting equation inserted into (1),
one obtains

Because of the assumption (b), we always have kr << kB in the far field, i.e.
for k0 > kr ; therefore

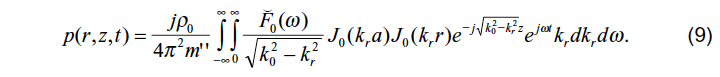
3.2. Evaluation of equation (9)
The integral over kr can be obtained from a comparison with the calculation of the radiation from a small piston membrane, and one can show that

Strictly speaking, this formula applies only if a is less than half a sound wavelength; along the symmetry axis, equation (10) also holds for larger values of a . Substitution of (10) into (9) gives

This surprisingly simple result says that the time history of the sound pressure near the symmetry axis corresponds exactly to the time history of the force acting on the plate and hence to the time history of the current in the moving coil. The time-lag due to sound wave propagation in the air is expressed by the argument

4. Conclusion
It can be shown theoretically, with the above simplifying assumptions, that the sound pressure radiated by a large, very pliable, damped plate along the symmetry axis, has a time history that corresponds to that of the excitation force in the moving coil (which has to be very light) and hence to the time history of the coil current. Therefore, time histories of currents with sudden changes (square wave) are reproduced correctly in the radiated sound pressure.

The time history of the sound pressure at positions off the symmetry axis can be obtained from the above equations only after lengthy numerical evaluations. Presumably, the gradual decay of the function J0(kra) for increasing arguments causes a "rounding-off of the corners in the time history" for small distances from the symmetry axis, and a completely different time history for points further away.

Download PDF